| Sections 12.1 and 12.2 |
1. True or false: On a weather map, there can be two isotherms which represent the same temperature but that do not intersect. (Explain your answer.)
2. True or fase: A function f(x,y) can have the property that g(x)=f(x,5) is increasing, whereas h(x)=f(x,10) is decreasing. (Explain your answer.)
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered?
|
| Section 12.3 |
1. Explain why the following statement is true: "the more closely spaced the contours, the steeper the terrain; the more widely spaced the contours, the flatter the terrain. The truth of this statement depends heavily on what convention about contour diagrams?
2. Suppose f(x,y)= x^2+y. Describe the contour set f(x,y)=3. What can you say, in general, about the contours of the function f?
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered?
|
| Section 12.4 |
1. Consider the values in the table below:
| x\y |
1 |
2 |
3 |
1 |
1 |
3 |
5 |
| 2 |
4 |
? |
8 |
| 3 |
7 |
9 |
11 |
Compute the value that would have to go in the center square if the function values are to correspond to a linear function of two variables. Explain how you got your answer.
2. What is the formula for the linear function of two variables that matches the entries in the table given in question 1?
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered?
|
| Section 12.6 |
1. Suppose that z=f(x,y) is a function of two variables. True or False: If the limit at (0,0) of the function along the cross section formed by the xz-plane and the limit at (0,0) of the function along the cross section formed by the yz-plane both exist and are equal, the limit of the function at (0,0) exists. Explain your answer.
2. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Sections 13.1 and 13.2 |
No real questions, but I need to know two things:
1. Experience shows that most people who take Calculus C have already seen this material at least in some form. (Doesn't mean they remember all of it!) Have you seen all or most of this material before? (Don't worry if the answer is no, I just need to know whether the ideas are new or review for you.)
2. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 13.3 |
1. True or false: If 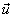 and and 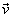 are vectors, then are vectors, then 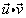 is a vector. is a vector.
2. True or false: For any vectors 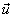 and and 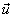 , then , then 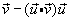 is perpendicular to is perpendicular to 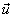 . .
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered?
|
| Section 13.4 |
1. True or false: 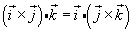
2. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 14.1 |
1. If f(x,y) is a function of two variables and fx (10,20) is defined, then fx (10,20) is a scalar quantity.
2. If fx (a,b )> 0, then the values of f decrease as we move in the negative x-direction near (a,b).
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 14.2 |
No real questions, but I need to know two things:
1. How confident are you with the rules for differentiating functions that you learned in first semester calculus? (This is for my information only, so that I can best help with partial differentiation.)
2.
Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 14.3 and 14.4 |
1. True or false: The function f(x,y) = y exp(x^2) is approximately equal to y near the point (0,1). Explain your answer.
2.
What is meant by the words "directional derivative"?
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered?
|
| Section 14.4 (again!) |
1. What is the (geometric) relationship between the level curves and the gradient vectors?
2. As you know, the gradient is a vector quantity. How can we interpret the magnitude and direction of the gradient?
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Sections 14.6 |
1. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 14.7 |
1. Suppose that I tell you that the mixed second partial derivatives of a function f are continuous everywhere and that fxy (x,y) = 2x cos(xy). What can you, then, conclude?
2. Suppose that f is a function of two variables and I tell you that fxx (3,2) >0. What does this tell you about the graph of the function f?
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 14.8 |
1. The definition given for differentiability for a function f(x,y) refers to a linear function L(x,y) and an error function E(x,y). How would we connect each of these with the intuitive idea we have discussed before of "zooming in" on a surface until we see something that looks like a plane?
2.
What is the relationship between continuity and differentiability for functions of two variables?
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered?
|
| Section 15.1 |
1. Look at the contour diagram shown in figure 15.11 on page 705. How many critical points does it show and where are they? Explain how you can tell.
2. Are the critical points shown in the contour diagram of figure 15.11 maxima, minima, or neither? Explain.
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered?
|
| Section 15.2 |
1. True or false: If the gradient of a function is zero at (a,b), then f has either a maximum or a minimum at the point (a,b). Explain.
2. True or false: If f(x,y) is a two-variable function defined on the Rectangle -1<=x<=1 and -1<=y<=1, then f has a global maximum and a global minimum on that rectangle.
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered?
|
| Section 15.3 |
1. The method of Lagrange multipliers tells us how to accomplish what mathematical task?
2. The method of Lagrange multipliers is based on the observation that two gradients are parallel? What gradients are they?
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 16.1 |
1. In first semester calculus, if we had a function defined on an interval, we divided the interval into subintervals and computed the area of a rectangle corresponding to each subinterval. The sum of the areas of these rectangles approximated the integral of the one-variable function over the interval in question. Give an analogous description of an approximation to a function of several variables over a rectangular region.
2. If the region of interest (as discussed in question 1) is not rectangular, how do we approximate the integral of the function over the region?
3.
Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 16.2 |
1. What is the significance of re-interpreting the integral of a function of two variables over a region as an iterated integral? (That is, why would we want to do this?)
2. How do we decide on the order in which to consider the variables in an iterated integral?
3. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 16.3 |
1. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 16.4 |
1. The infinitessimal dA in rectangular coordinates is sometimes represented as dx dy. Why is this a reasonable representation? What is the "parallel" representation for functions written in polar coordinates? Why the difference?
2. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 16.5 |
1. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 17.1 & 17.2 |
1. In example 1 of 17.2 (ferris wheel example), which of the following is true:
a. The child's speed is constant.
b. The child's velocity is constant.
c. The child's acceleration is constant.
d. All of the above.
e. Only a) and b).
Explain your answer.
2
. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Sections 17.3 and 17.4 |
1. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 18.1 |
1. Give an intuitive description of what a line integral measures.
2. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |
| Section 18.2 |
1. Was there a specific section that was confusing to you? Is there any specific (or general) question you would like to have answered? |