Evaluating Integrals in Maple 

To evaluate an indefinite integral in Maple, use the command "int(f(x),x)".  The "int" command tells Maple to integrate, the "f(x)" term is the function you want to integrate, and the last "x" tells Maple that you want to integrate with respect to the variable x.  Note that Maple does not include the constant of integration, so you'll need to remember to do that.   

>

 

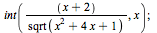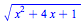(1)

 

>

 

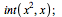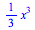(2)

 

>

 

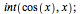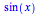(3)

 

>

 

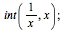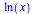(4)

 

You can also use the graphical toolbar on the left of your Maple window to evaluate indefinite integrals. 

>

 

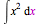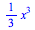(5)

 

To evaluate a definite integral in Maple, use the command "int(f(x),x=a..b)", where a is your lower bound of integration and b is your upper bound of integration. 

>

 

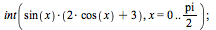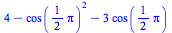(6)

 

>

 

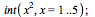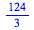(7)

 

You can also use the graphical toolbar on the left of your Maple window to evaluate definite integrals. 

>

 

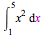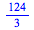(8)

 

>