Maple worksheet for implementing Euler's method
First, call the "DEtools" and "plots" packages.
| > |
Define the differential equation that you want to study.
| > |
| (1) |
Specify the initial conditions.
| > |
| (2) |
Specify the step size and the total number of steps that you want to take.
| > |
| (3) |
Implement the method (and create a plot of the results).
| > |
| (4) |
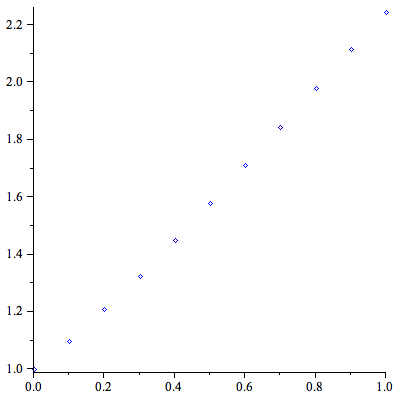
Display the plot of the numerical results of Euler's method.
| > |
 |
| > |